[TOC]

HNCTF

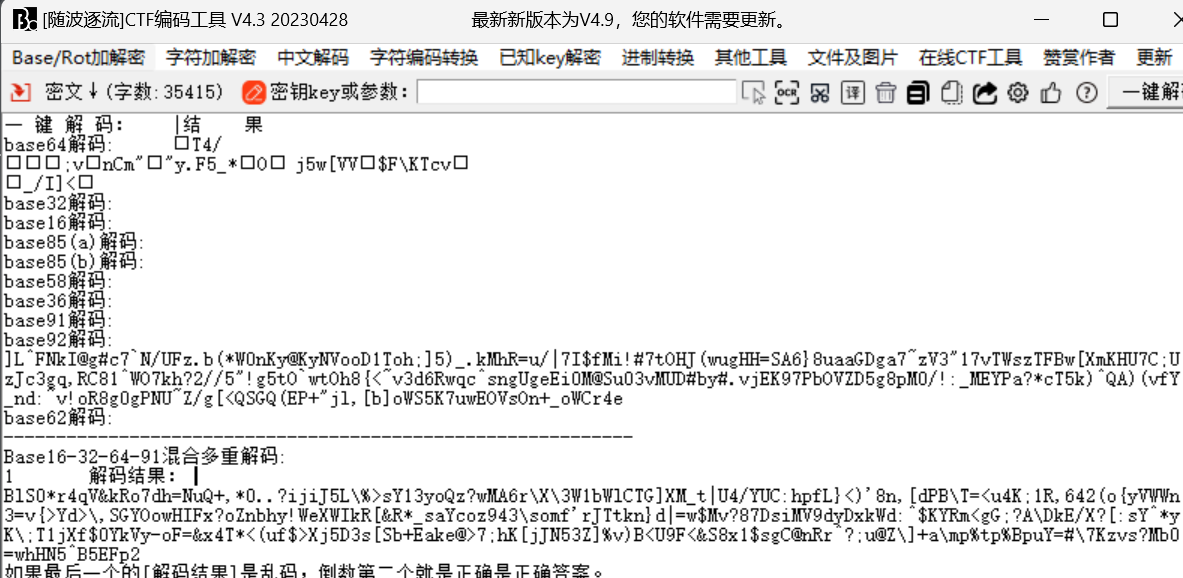
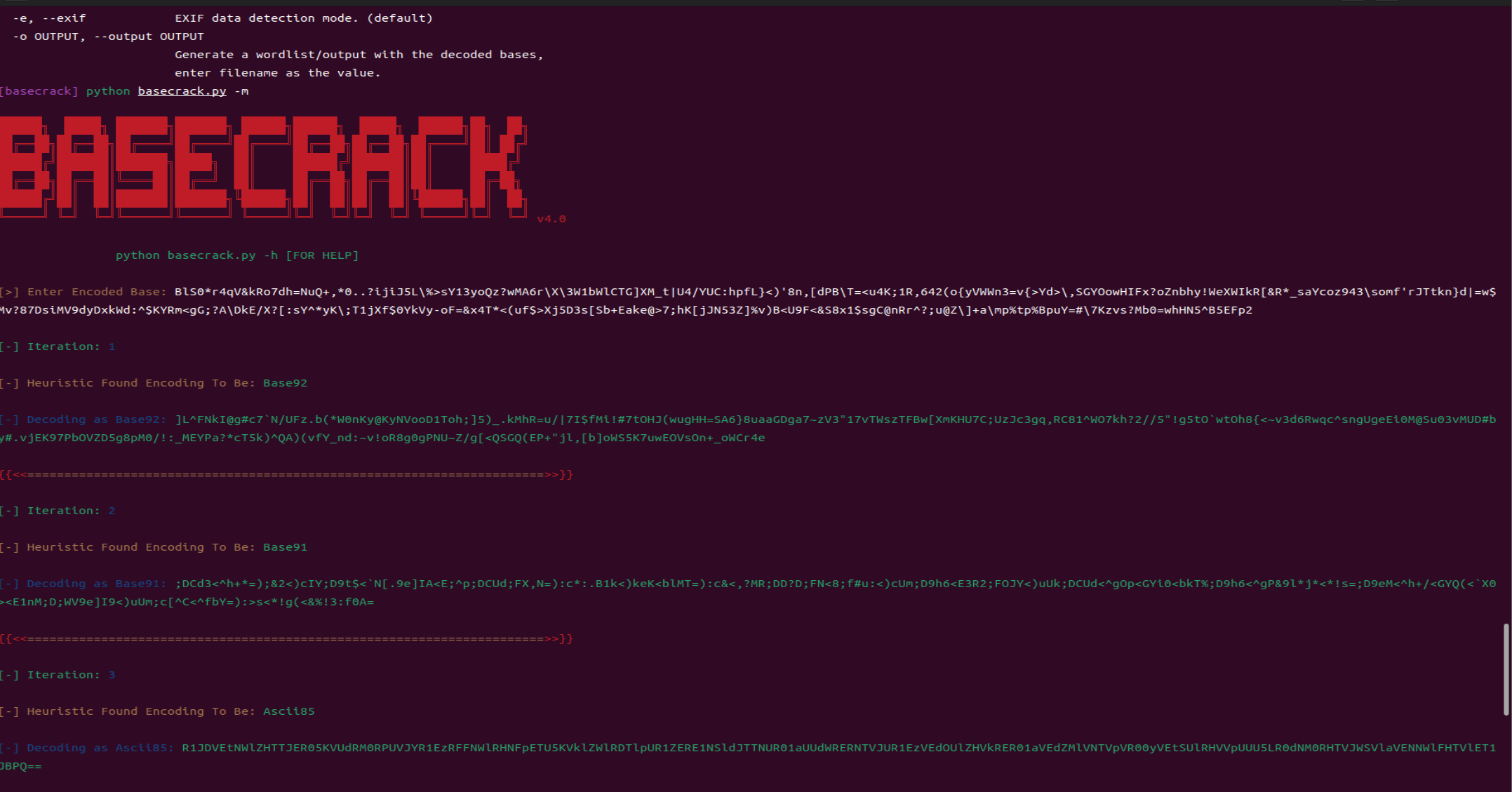
baBAbaseSEse（base家族）

base家族

  • 随波逐流梭哈

  • basecrack一把梭，windows我装不上，然后我就装到ubuntu了

babyRsa（基本RSA）

基础知识

注意：这里不能安装其他库，不然会因为版本问产生一系列的兼容性问题

  1. PyCryptodome库主要由以下模块组成：
  • Crypto.Cipher：包含对称加密算法，如AES、DES等。
  • Crypto.PublicKey：包含非对称加密算法，如RSA、DSA等。
  • Crypto.Hash：包含哈希函数，如SHA256、MD5等。
  • Crypto.Signature：包含数字签名相关功能。
  • Crypto.Random：提供随机数生成器。
  • Crypto.Protocol：包含各种协议实现，如PBKDF2。
  • Crypto.Util：包含一些实用工具，如填充、字节处理等

  1. 对于RSA的一些工具

    • YAFU： YAFU（Yet Another Factoring Utility）是一个开源的用于整数因数分解的命令行工具。它是一个强大而灵活的工具，能够分解大整数为其质因数，有助于解决数论和密码学领域中的问题。YAFU是基于GMP（GNU多精度算法库）的，并使用了多种因数分解算法来优化分解过程。它是数学爱好者、密码学研究人员和密码分析者常用的工具之一

      1
      2
      3
      1.使用 cmd 进入到 yafu 所在目录下，或将目录加入到系统环境 PATH 变量，或打开目录文件夹后 shift+右键 选择在此处打开 powershell 
      2.假如要分解因数 6 ，输入命令：.\yafu-x64.exe "factor(6)"
      3.如果因数过长，将 因数 用文本文件存放在 yafu 目录下，例如：data.txt 。文件最后一行一定要换行，否则eof; done processing batchfile。 运行命令：.\yafu-x64.exe "factor(@)" -batchfile data.txt

    • FactorDB： FactorDB是一个在线的整数因数分解数据库。它允许用户将大整数提交到数据库，并查找其质因数分解。这个数据库是由全球用户提交的整数分解结果共同维护的，它采用了多种现代算法来分解整数。FactorDB 对于那些没有自己的因数分解工具或想要验证分解结果的用户来说是非常有用的。通过FactorDB，用户可以快速地找到一个整数的质因数，而无需自行进行因数分解运算 网站factordb.com

    这个题是一个简单的RSA

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    from Crypto.Util.number import bytes_to_long, getPrime
    # 这里我们导入了bytes_to_long函数，它用于将字节转换为长整数（将flag转换为m），以及导入了getPrime函数，它用于生成指定位数的随机素数。
    from gmpy2 import *
    P39 = 265147241000574873803071047177766359643
    P39 = 234560843346150602519484260867514743467
    q = getPrime(128)
    p = getPrime(128)
    # 这两行代码使用getPrime(128)函数生成两个128位的随机素数，并将它们赋值给变量p和q。在RSA加密中，p 和 q 是用于计算 RSA 公钥和私钥的重要参数。
    n = p * q
    e = 65537
    c = 17331436837911040930486942133359735652484926528331507431552667656734821231501
    # n 是RSA的模数，它是两个素数 p 和 q 的乘积。
    # e 是RSA的公钥指数，通常为固定值 65537（也称为常用的 RSA 公钥指数）。
    # c 是RSA的密文，通过用公钥指数 e 对明文 m 进行模幂运算得到。
    print(n,c)
    # 62193160459999883112594854240161159254035770172137079047232757011759606702281
    # 17331436837911040930486942133359735652484926528331507431552667656734821231501

    通过上述工具进行分解之后，然后写出对应的解密脚本即可，这里主要是了解了这些库的一些基本使用而已

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    计算 RSA 私钥参数：
    使用已知的 p 和 q 计算了模数 n，并通过调用 invert(e, (p-1)*(q-1)) 函数计算得到私钥指数 d。
    RSA 解密并输出明文：
    使用得到的私钥指数 d 和模数 n，将密文 c 进行 RSA 解密，并通过 long_to_bytes 函数将解密后的长整数转换为明文，并进行输出。
    from Crypto.Util.number import bytes_to_long, getPrime, long_to_bytes
    from gmpy2 import *
    e = 65537
    p = 234560843346150602519484260867514743467
    q = 265147241000574873803071047177766359643
    c = 17331436837911040930486942133359735652484926528331507431552667656734821231501
    n = p * q
    d = invert(e,(p-1)*(q-1))
    print(long_to_bytes(pow(c,d,n)))

    然后安装了sage的软件，还没有使用，明天再看看吧！

A dictator（凯撒密码）

凯撒密码就是根据偏移移位的密码

加密过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from random import randint
from secret import flag

# # 用于生成一个在范围 [1, 100] 内的随机整数，并将其对 26 取模，以确保得到的偏移量在 0 到 25 之间
offset = randint(1,100) % 26
print(offset)

assert flag.startswith('NSSCTF{')
# 确保flag字符串中除去前7个字符和最后一个字符的部分，所有字符都不是大写字母
assert all([ord(c) not in range(ord('A'),ord('Z')) for c in flag[7:-1]])

for char in flag[7:-1]:
    if ord('a') <= ord(char) <= ord('z'):
        # 小写字母计算偏移量
        index = ord(char)-ord('a')
        # 计算新的字符
        new_char = chr((index+offset)%26 + ord('a'))
        print(new_char,end='')
    else:
        print(char,end='')
# 密文
# cipher = 'nby_wuymul_wcjbyl_cm_ihy_iz_nby_gimn_vumcw_wfummcwuf_wcjbylm'

解密过程：这个加密解密完都是小写字母，通过25个随机数字进行爆破解密即可

1
2
3
4
5
6
7
8
9
10
11
cipher = 'nby_wuymul_wcjbyl_cm_ihy_iz_nby_gimn_vumcw_wfummcwuf_wcjbylm'
# 从0-25遍历
for offset in range(26):
    print()
    for i in cipher:
        if ord('a') <= ord(i) <= ord('z'):
            index = ord(i) - ord('a')
            new_char = chr((index + offset) % 26 + ord('a'))
            print(new_char, end='')
        else:
            print(i, end='')

官方wp有一个string的库，这里学习了一下

问：from string import ascii_lowercase string库是什么库？

答：在Python中，string 是一个标准库，它包含了许多与字符串处理相关的常用常量和函数。通过导入 string 库，你可以使用其中定义的常量和函数，而不需要自己定义相同的内容。

在给定的代码中，使用 from string import ascii_lowercase 导入了 string 标准库中的 ascii_lowercase 常量。ascii_lowercase 是一个包含所有小写字母的字符串，它的值为 'abcdefghijklmnopqrstuvwxyz'。这样一来，代码就可以直接使用 ascii_lowercase 变量来表示小写字母表，而不需要手动定义这个字符串。

爱妃（仿射密码）

放射密码（Affine Cipher）是一种古典密码学中的替换密码，它对字母表中的字符进行加密和解密。放射密码的数学原理涉及到仿射函数的应用。

放射函数的一般形式为：E(x) = (ax + b) mod m

其中：

  • E(x) 表示密文字符；
  • x 表示明文字符；
  • a 和 b 是整数，并且满足 a 和 m 互质（最大公约数为1）；
  • mod m 表示对 m 取模，即结果在 0 到 (m-1) 的范围内。

在放射密码中，每个明文字符 x 被映射为一个密文字符 E(x)。参数 a 和 b 是放射函数的密钥，通过正确选择这些密钥，可以实现有效的加密和解密。

解密过程是对密文字符应用逆放射函数：D(y) = a^(-1) * (y - b) mod m，其中 a^(-1) 表示 a 的乘法逆元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import gmpy2

def decrypt(cipher, a_invert, b, m):
    return bytes([a_invert*(i   - b) % m for i in cipher])
def encrypt(message, a, b, m):
    return bytes([(ord(i) * a + b) % m for i in message])

c = b'y\xba\xba\xea\xc7\x11\xc2\xc7\xcb\xd8ZV\xd8ZVp\xb1\xb1\xd8\x19\xa4V\xa4\x19\x8aM\xa83g\xd8&\x19\xdc'
flag = 'NSSCTF{'
# 计算密钥a，b
for a in range(m):
    for b in range(m):
        if encrypt(flag, a, b, m) in c:
            pass
 			# print(a, b)
m = 1 << 8
a = 13 
b = 131
# 计算a的逆元函数
a_invert = gmpy2.invert(13,256)
print('a_invert = ', a_invert)
m = decrypt(c,a_invert,b,m)
print(m.decode('utf-8'))
print(str(m))

littleprince(同余方程，中国剩余定理)

这道题的给的加密代码有一些难理解，在这里记录一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from secret import flag
from Crypto.Util.number import *
from random import randint


def enc(a, b, c):
  	# 1 << b 表示将数字 1 左移 b 位，即得到一个只有第 b 位为1，其余位都为0的整数
    # 例如，如果 b 等于 3，那么 1 << b 就等于二进制数 0b1000，也就是十进制数 8	
	# 对结果 1 << b 减去 1，这样得到的二进制数将会是从第 0 位到第 b-1 位都是1，其余位都是0
	# 以 b 等于 3 为例，((1 << 3) - 1) 将得到二进制数 0b111，也就是十进制数 7
	# 最后，我们将 a 和上述得到的结果进行按位与操作 &，这样就会保留 a 的低 b 位，将其余高位都置为0
    # a的低b位的掩码在这里保留a的最后b位置，其他位置设为0
    # 它将这两个结果进行位或操作 | 并将低 c - b 位左移
    # 目的是对a进行加密并且返回
    return a >> b | (a & ((1 << b)-1)) << (c-b)


def outp(x, h):
    p = randint(1 << h, 1 << h+1)
    q = randint(1 << h, 1 << h+1)
    c1, c2 = x % p, x % q
    print(p, q, c1, c2)

# flag 转成长整数m
m = bytes_to_long(flag)
# 计算m的二进制位数
m_len = m.bit_length()
d, h, st = 32, 16, 32
r = m_len % d
assert (r > h)
while st <= m_len:
    # 对m进行加密
    x = enc(m, st, m_len)
    x >>= (m_len-d)
    # 输出加密结果
    outp(x, h)
    st += d
# 对 m 进行额外的加密操作，并通过 outp 函数输出最终的加密结果
m >>= (m_len-r)
outp(m, h)

掩码

在计算机科学中，”掩码”（Mask）是一个用于屏蔽或提取某些位的二进制模式。掩码通常是一个与目标数据进行按位与操作的值，通过这种操作，可以将目标数据的某些位设置为0或从中提取出感兴趣的位。

掩码在计算机编程和计算机系统中有广泛的应用，主要用于以下两个方面：

  1. 屏蔽位：掩码可以用于屏蔽目标数据的特定位。通过将目标数据与相应的掩码进行按位与操作，可以将不需要的位设置为0，而保留需要的位。这在编程中常用于清除或保留特定标志位，或者过滤掉数据中不需要的部分。
  2. 提取位：掩码还可以用于从目标数据中提取出感兴趣的位。通过将目标数据与相应的掩码进行按位与操作，可以将目标数据的其他位设置为0，而保留感兴趣的位。这在计算机系统中常用于从寄存器或数据中提取出特定字段或标志位。

掩码通常使用二进制形式表示，并且每个位都对应于目标数据的相应位。在掩码中，1 表示需要保留或提取的位，0 表示需要屏蔽的位。

例如，对于目标数据 11010110，如果我们希望屏蔽掉低三位，我们可以使用掩码 11111000，通过进行按位与操作，结果将是 11010000。同样，如果我们希望提取低四位，我们可以使用掩码 00001111，通过进行按位与操作，结果将是 00000110。

  • 总结：与运算取出感兴趣的位，感兴趣为1，不感兴趣为0

关于移位

a >> b | (a & ((1 << b)-1)) << (c-b)

假设 a 等于 87 （二进制：0b1010111），b 等于 4。

  1. 1 << b 的结果为 0b10000，也就是十进制数 16。
  2. ((1 << b) - 1) 的结果为 0b1111，也就是十进制数 15。
  3. a & ((1 << b) - 1) 就是 0b1010111 & 0b1111，结果为 0b111，也就是十进制数 7。

所以，(a & ((1 << b) - 1)) 表达式的结果就是 a 的低 b 位的掩码，它将保留 a 二进制表示中的最后 b 位，并将其他位设置为0。

RSA系列

RSA原理

生成数字

加密与解密

RSA Py代码实现

Python代码的计算过程

  1. 导入子库生成两个大素数，512bit朝

    1
    2
    3
    4
    5
    6
    from Crypto.Util.number import *
    # getPrime函数，它能够返回一个n位的素数
    p = getPrime(512)
    q = getPrime(512)
    print(p)
    print(q)

  2. 计算欧拉函数和n

    1
    2
    n = p*q
    phi = (p-1)*(q-1)

  3. 选取e判断互素性，并且计算逆元

    1
    2
    3
    e = 65537
    assert GCD(e, phi) == 1, "该e不满足互素条件"
    d = inverse(e, phi)

  4. 加密hello

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    # 这里定义的是byte类型的字符串，每个字符用8位的二进制进行存储，如果直接定义字符串hello，字符串类型需要进行编码字节类型才可以进行加密
    message = b'hello'
    # 使用的bytes_to_long函数，将字符串转换为数字
    m = bytes_to_long(message)
    print(m)
    # 消息已经被转换为一个字符串了，可以加密
    c = pow(m, e, n)
    print(c)
    # 解密
    msg = pow(c, d, n)
    print(msg)

  5. 完整代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    from Crypto.Util.number import *
    p = getPrime(512)
    q = getPrime(512)

    n = p*q
    phi = (p-1)*(q-1)
    e = 65537
    assert GCD(e, phi) == 1, "该e不满足互素条件"
    d = inverse(e, phi)

    print(f'公钥：({e}, {n})')
    print(f'私钥：({d}, {n})')

    message = b'hello'
    m = bytes_to_long(message)
    print('消息：', m)

    c = pow(m, e, n)
    print('密文：', c)

    msg = pow(c, d, n)
    print('明文：', msg)

    assert msg == m, "解密失败"

RSA类型

p-q过小差值小类型

题目代码

1
2
3
4
5
6
7
8
9
from Crypto.Util.number import *
import gmpy2
flag = b'NSSCTF{******}'
# 特征
p = getPrime(512)
q = gmpy2.next_prime(p)
n = p*q
e = 65537
phi = (p-1)*(q-1)

这里一个特征就是，p通过函数生成512位的素数，然后q为其相邻的下一个素数，可以进行测试

1
2
3
4
5
from Crypto.Util.number import *
import gmpy2
p = getPrime(512)
q = gmpy2.next_prime(p)
print(q-p)

解题原理

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
from Crypto.Util.number import *
from gmpy2 import *
n =
e = 
c = 
sn = gmpy2.isqrt(n)
q = gmpy2.next_prime(sn)
p = n // q
e = 65537
phi = (p-1)*(q-1)
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))

费马分解

对称密码系列

定义：对称加密，称为对称密码,是指在加密和解密时使用同一密钥得加密方式。

特点：比非对称加密要快

DES

典型的块加密，将明文分块加密

特点

在DES中，具有如下特点

  1. 输入64位
  2. 输出64位
  3. 密钥64位，使用64位密钥中的56位，剩余的8位要么丢弃，要么作为奇偶校验位
  4. 采用Feistel迭代结构：
    1. 明文经过 16 轮迭代得到密文
    2. 密文经过类似的 16 轮迭代得到明文

加密过程

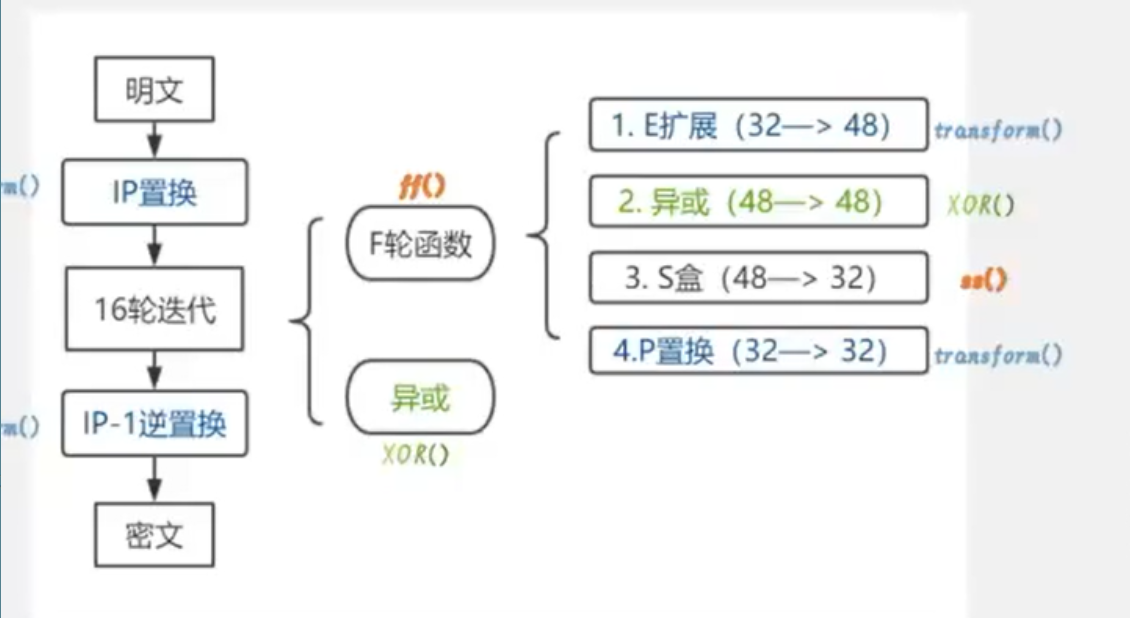
初始IP置换

  • 64位明文分组X经过一个初始置换函数IP，产生64位的输出X0，再将分组X0分成左半部分L0和右半部分R0。
    1. 将输入的第58位换到第一位，第50位换到第2位，…，依次类推。
    2. L0、R0则是换位输出后的两部分， L0是输出的左32位， R0是右32位。
  • 简而言之，这就是打乱了明文之间的排列，我们使用Python来实现这个函数，在这里及后续的代码中，我们都将明文认为是一个数字数组进行操作。

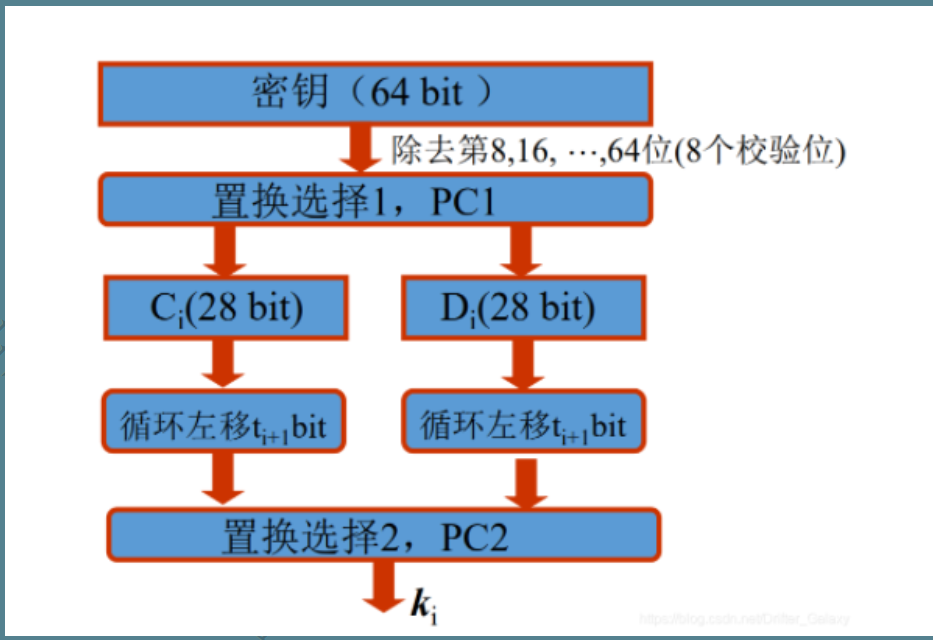
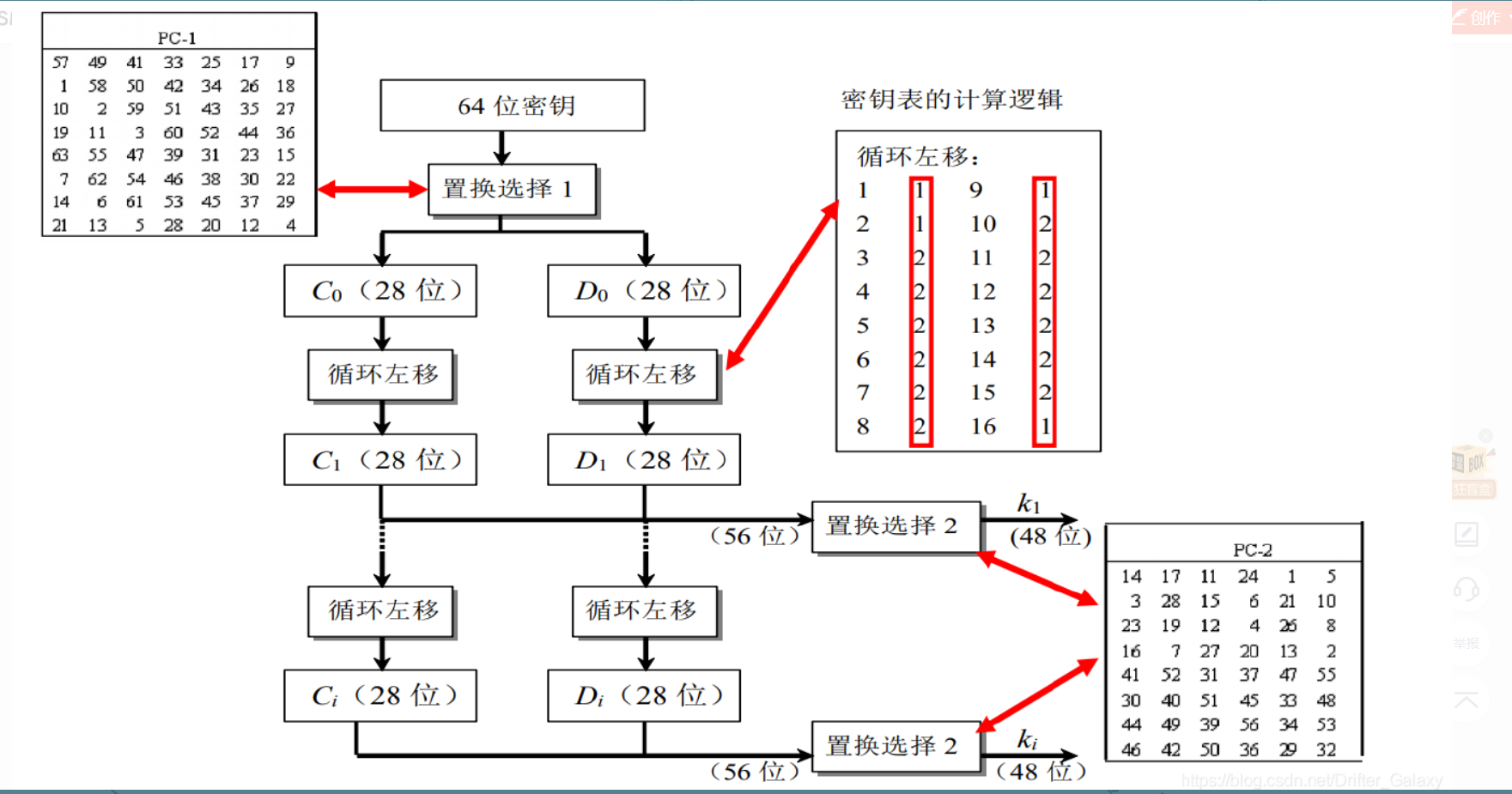
获取子密钥

  • 在进入第一轮之前，我们还需要对密钥进行处理生成子密钥，每一轮将使用不同的子密钥参与运算。DES加密算法的密钥长度为56位，一般表示为64位(每个第8位用于奇偶校验)，将用户提供的64位初始密钥经过一系列的处理得到K1,K2,…,K16，分别作为1~16轮运算的16个子密钥。

    1. 将64位密钥去掉8个校验位，用密钥置换PC-1置换身下的56位密钥

    2. 将56位分成前28位和后28位

    3. 根据轮数，将这两部分别循环左移1位或2位

    4. 移动后，将两部分合成56位后压缩置换PC-2后得到48位子密钥

密码函数F

  • 密码函数F的作用是将输入的32比特数据和48比特子密钥进行加密输出32比特

    1. 扩展置换E：将数据的右半部分Ri从32位扩展为48位。位选择函数(也称E盒)
    2. 异或：扩展后的48位输出E(Ri)与压缩后的48位密钥Ki作异或运算
    3. S盒替换：将异或得到的48位结果分成八个6位的块，每一块通过对应的一个S盒产生一个4位的输出
    4. P盒置换：将S盒得到的输出再和P盒进行置换操作

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
from operator import add
from typing import List
from functools import reduce
# operator这个库提供了一组函数，用于执行Python内置运算符的操作。它允许您以函数的形式使用像加法、减法、乘法等运算符，从而使您能够以更灵活的方式操作数据。例如，add()函数允许您将两个数字相加，而不是使用+运算符
# typing提供了在Python中进行类型提示(type hinting)的功能。允许开发者在函数参数、返回值和变量上添加类型注释。
# 这个库提供了一些函数式编程工具，它们可以让您更轻松地处理函数和操作。其中最常用的函数是reduce()，它可以对一个序列中的元素应用某个二元函数，并返回一个最终的聚合结果
_IP = [
    57, 49, 41, 33, 25, 17, 9,  1,
	59, 51, 43, 35, 27, 19, 11, 3,
	61, 53, 45, 37, 29, 21, 13, 5,
	63, 55, 47, 39, 31, 23, 15, 7,
	56, 48, 40, 32, 24, 16, 8,  0,
	58, 50, 42, 34, 26, 18, 10, 2,
	60, 52, 44, 36, 28, 20, 12, 4,
	62, 54, 46, 38, 30, 22, 14, 6
]
# 这里的plain：List[int]是类型注释，代表plain的参数应该是一个整数列表 但注意，这只是一种提示，并不是强制执行这些类型
# map用于可迭代对象中每个元素给定的函数
# lambda 匿名函数 参数x，返回plain[x]
# 函数功能介绍，将_IP中每个元素作为索引x获取plain[x] 
def IP(plain: List[int]):
    return list(map(lambda x: plain[x], _IP))

# 获取子密钥
# 置换56位密钥的pc-1置换表
__pc1 = [56, 48, 40, 32, 24, 16,  8,
	  0, 57, 49, 41, 33, 25, 17,
	  9,  1, 58, 50, 42, 34, 26,
	 18, 10,  2, 59, 51, 43, 35,
	 62, 54, 46, 38, 30, 22, 14,
	  6, 61, 53, 45, 37, 29, 21,
	 13,  5, 60, 52, 44, 36, 28,
	 20, 12,  4, 27, 19, 11,  3
]
# 移动后合并56位压缩置换pc-2置换表
__pc2 = [
	13, 16, 10, 23,  0,  4,
	 2, 27, 14,  5, 20,  9,
	22, 18, 11,  3, 25,  7,
	15,  6, 26, 19, 12,  1,
	40, 51, 30, 36, 46, 54,
	29, 39, 50, 44, 32, 47,
	43, 48, 38, 55, 33, 52,
	45, 41, 49, 35, 28, 31
]

# 循环左移轮数对应于1位或2位
ROTATIONS = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]

# PC_1置换函数
def PC_1(key: List[int]):
    return list(map(lambda x: key[x], __pc1))

# PC_2置换函数
def PC_2(key: List[int]):
    return list(map(lambda x: key[x], __pc2))


# 获取子钥
def get_sub_key(key: List[int]):
    key = PC_1(key) # PC-1置换
    L, R = key[:28], key[28:] # 分成两半
    skeys = []
    for i in range(16):
        for j in range(ROTATIONS[i]): # 根据轮次左移
            L = L[1:] + L[:1]
            R = R[1:] + R[:1]
        skeys.append(PC_2(L+R)) # PC-2置换
    return skeys
# E扩展
__expansion_table = [
	31,  0,  1,  2,  3,  4,
	 3,  4,  5,  6,  7,  8,
	 7,  8,  9, 10, 11, 12,
	11, 12, 13, 14, 15, 16,
	15, 16, 17, 18, 19, 20,
	19, 20, 21, 22, 23, 24,
	23, 24, 25, 26, 27, 28,
	27, 28, 29, 30, 31,  0
]
# S置换
__sbox = [
		# S1
		[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
		 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
		 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
		 15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],

		# S2
		[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
		 3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
		 0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
		 13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],

		# S3
		[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
		 13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
		 13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
		 1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],

		# S4
		[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
		 13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
		 10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
		 3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],

		# S5
		[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
		 14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
		 4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
		 11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],

		# S6
		[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
		 10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
		 9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
		 4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],

		# S7
		[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
		 13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
		 1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
		 6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],

		# S8
		[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
		 1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
		 7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
		 2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11],
	]
# P置换
__p = [
	15, 6, 19, 20, 28, 11,
	27, 16, 0, 14, 22, 25,
	4, 17, 30, 9, 1, 7,
	23,13, 31, 26, 2, 8,
	18, 12, 29, 5, 21, 10,
	3, 24
]

def EP(data: List[int]):  # E扩展置换
    return list(map(lambda x: data[x], __expansion_table))

def P(data: List[int]):   # P置换
    return list(map(lambda x: data[x], __p))

def F(index: int, R: List[int], skeys: List[List[int]]):
    """
    index: 代表这是第几轮
    R: 输入数据
    skeys: 子密钥数组
    """
    # 第一步 E扩展 32位-48位
    R = EP(R)  # 扩展置换
    # 第二步 和48位密钥异或 
    R = list(map(lambda x, y: x ^ y, R, skeys[index]))  # 异或
    # 第三步 s盒压缩处理  48bit -> 32bit
    B = [R[:6], R[6:12], R[12:18], R[18:24], R[24:30], R[30:36], R[36:42], R[42:]]  # 分成八份
    Bn = [0] * 32
    pos = 0
    for i in range(8):
        #  计算该使用S盒的行坐标和列坐标
        row = (B[i][0] << 1) + B[i][5]
        col = (B[i][1] << 3) + (B[i][2] << 2) + (B[i][3] << 1) + B[i][4]
        sb = __sbox[i][(row << 4) + col]
        # 六位置
        Bn[pos + 0] = (sb & 8) >> 3  
        Bn[pos + 1] = (sb & 4) >> 2
        Bn[pos + 2] = (sb & 2) >> 1
        Bn[pos + 3] = (sb & 1)
        pos += 4
        
    # 第四步 P置换  32-32
    R = P(Bn)
    return R

_FP = [
	39,  7, 47, 15, 55, 23, 63, 31,
	38,  6, 46, 14, 54, 22, 62, 30,
	37,  5, 45, 13, 53, 21, 61, 29,
	36,  4, 44, 12, 52, 20, 60, 28,
	35,  3, 43, 11, 51, 19, 59, 27,
	34,  2, 42, 10, 50, 18, 58, 26,
	33,  1, 41,  9, 49, 17, 57, 25,
	32,  0, 40,  8, 48, 16, 56, 24
]

# 逆置换，相对于初始置换的逆操作，将数据放回原位
def FP(plain: List[int]):
    return list(map(lambda x: plain[x], _FP))
# =================================================================================================================
# 密钥
key = b'12345678'
# 加密内容
plain = b'12345678'

# 转为二进制数组
key = reduce(add, [list(map(int, bin(i)[2:].zfill(8))) for i in key])
plain = reduce(add, [list(map(int, bin(i)[2:].zfill(8))) for i in plain])
skeys = get_sub_key(key)

# 初始IP置换
block = IP(plain)
# 分为左右32比特得到L1，R1
L, R = block[:32], block[32:]
# 16轮迭代
for i in range(16):
    # 复制整个字符串
    tpR = R[:]
    # R0 和 key1进行轮函数得R1
    R = F(i, R, skeys)
    # R1 和 L0 进行异或
    R = list(map(lambda x, y: x ^ y, R, L))
    # 复制R1给L1
    L = tpR
# 合并16轮之后的左右部分(L16和R16)
block = R + L
# 逆置换
block = FP(block)
# 输出结果
enc = bytes([int(''.join(map(str,block[i*8:(i+1)*8])),2) for i in range(8)])
print(enc)

封装库实现

1
2
3
4
5
from Crypto.Cipher import DES
des = DES.new(b'12345678', DES.MODE_ECB)
print(des.encrypt(b'12345678'))
m = des.encrypt(b'12345678')
print(des.decrypt(m))

AES

特点

  1. 输入：128 比特。
  2. 输出：128 比特。
  3. SPN 网络结构。

与DES的注意点

  1. 每一刻从64位变成128位
  2. AES采用的的SPN网络结构与Feistel相比，可以加密整个块，并且解密必须是对加密的逆运算
  3. SPN全称为Substitution-permutation network即代换-置换网络，简单的说就是会对块进行替换，置换等多重迭代操作。

迭代过程

  1. AddRoundKey轮密钥加
  2. SubBytes字节替换
    这里引入一个S盒，然后进行S盒替换
  3. ShiftRows行位移变换
    这也是一次扩散处理，达到雪崩效应（雪崩效应是指当输入发生最微小的改变（例如，反转一个二进制位）时，也会导致输出的不可区分性改变，即扩大错误防止攻击者找到不同明密文之间的关系）。
  4. MixColumns列混合变换
    也是扩散操作
  5. 子密钥生成

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
r_con = (0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,0x80, 0x1B, 0x36)
s_box = (
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)

def xor_bytes(a, b):
    return bytes(i^j for i, j in zip(a, b))

def add_round_key(s, k):
    for i in range(4):
        for j in range(4):
            s[i][j] ^= k[i][j]

def sub_bytes(s):
    for i in range(4):
        for j in range(4):
            s[i][j] = s_box[s[i][j]]

def shift_rows(s):
    s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]

# 参考 http://cs.ucsb.edu/~koc/cs178/projects/JT/aes.c
xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)

def mix_single_column(a):
    # see Sec 4.1.2 in The Design of Rijndael
    t = a[0] ^ a[1] ^ a[2] ^ a[3]
    u = a[0]
    a[0] ^= t ^ xtime(a[0] ^ a[1])
    a[1] ^= t ^ xtime(a[1] ^ a[2])
    a[2] ^= t ^ xtime(a[2] ^ a[3])
    a[3] ^= t ^ xtime(a[3] ^ u)

def mix_columns(s):
    for i in range(4):
        mix_single_column(s[i])

def _expand_key(s):
    for i in range(10):
        word = list(s[-1])  # 取得最后一列
        word.append(word.pop(0)) # 将首位移动到最后
        word = [s_box[b] for b in word]  # SubBytes操作
        word[0] ^= r_con[i]  # 和异或表内数据异或

        s.append(xor_bytes(word, s[-4]))  # 得到新的子密钥
        s.append(xor_bytes(s[-1], s[-4]))  # 因为直接在s中添加，所以本该和上一轮第二列异或的位置还是-4
        s.append(xor_bytes(s[-1], s[-4]))
        s.append(xor_bytes(s[-1], s[-4]))

    return [s[4*i : 4*(i+1)] for i in range(len(s) // 4)]

def bytes2matrix(text):
    """ Converts a 16-byte array into a 4x4 matrix.  """
    return [list(text[i:i+4]) for i in range(0, len(text), 4)]

key = b'1234567812345678'
plain = b'1234567812345678'
skeys = _expand_key(bytes2matrix(key))
plain = bytes2matrix(plain)

add_round_key(plain, skeys[0])

for i in range(1, 10):
    sub_bytes(plain)
    shift_rows(plain)
    mix_columns(plain)
    add_round_key(plain, skeys[i])

sub_bytes(plain)
shift_rows(plain)
add_round_key(plain, skeys[-1])

enc = bytes(plain[0]+plain[1]+plain[2]+plain[3])
print(enc)  # b'm\xac\x1cV\xe7G\xfa\xe0:\xcf\x8ch\x91\xe4(\xe0'

封装库实现

1
2
3
4
5
6
key = b'1234567812345678'
plain = b'1234567812345678'
from Crypto.Cipher import AES
cipher = AES.new(key, AES.MODE_ECB)
enc = cipher.encrypt(plain)
print(enc)

P1 DES 解密

知识点：DES的F函数可逆，改变一点就可以

  1. 无需关注F函数实现，查看16轮迭代

    1
    2
    3
    4
    5
    6
    L, R = block[:32], block[32:]
    for i in range(16):
        tpR = R[:]
        R = F(i, R, skeys)
        R = list(map(lambda x, y: x ^ y, R, L))
        L = tpR

  2. 代码实现，将代码逆过来即可

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    ​```
    1. 先IP置换函数
    2. 十六轮逆过程
    3. FP置换函数
    ​```
    # 加密代码
    L, R = block[:32], block[32:]
    for i in range(16):
        tpR = R[:]
        R = F(i, R, skeys)
        R = list(map(lambda x, y: x ^ y, R, L))
        L = tpR
    # 解密代码
    L, R = block[:32], block[32:]
    for i in range(15, -1, -1):
        tpR = R[:]
        R = F(i, R, skeys)
        R = list(map(lambda x, y: x ^ y, R, L))
        tpR = L

P2 DES 无密钥

1
2
3
4
5
def F(index: int, R: List[int], skeys: List[List[int]]):
    R = EP(R)  # 扩展置换
	# 比较代码没有和子密钥进行异或 直接进行解密
	# R = list(map(lambda x, y: x ^ y, R, skeys[index]))  # 异或
	B = [R[:6], R[6:12], R[12:18], R[18:24], R[24:30], R[30:36], R[36:42], R[42:]]  # 分成八份

P3 DES 密钥爆破

给出L和R和C R缺8位 爆破

1
2
3
L = [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1]
R = [0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
b'\x1d\xe8\xd1\xc8\x95{]\xa0'
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for i in range(2**8):
    R = RR +list(map(int, bin(i)[2:].zfill(8)))
    skeys = get_sub_key(LL, R)
    block = IP(enc)   
    L, R = block[:32], block[32:]
    for i in range(15, -1, -1):
        tpR = R[:]
        R = F(i, R, skeys)
        R = list(map(lambda x, y: x ^ y, R, L))
        L = tpR
    block = R + L
    block = FP(block)
    plain = bytes([int(''.join(map(str, block[i*8:(i+1)*8])), 2)for i in range(8)])
    flag = b'NSSCTF{%s}' % (plain)
    print(flag)

P4 DES Kn泄露

1
2
3
4
5
6
import pyDes
enc = b'3\xb3\xdc\xbfkg\x1b\xceG!\x08\x16\xf6i\x0c\xbd\xde_\xe7#\xe2\x99\xe7\xf0\xd9\x02\xd6Hi=1='
Kn = [```]
des = pyDes.des('11111111', padmode=pyDes.PAD_PKCS5)
des.Kn = Kn
print(des.decrypt(enc))

P4 DES Kn泄露 子密钥算法逆向

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
import pyDes

enc = b'\xed\xb7H\xa8zL\xb5\xff\xb2g\x1c<\x17G^\xda\xd4\xb2\x84X\xb4\x92\x18I\xaf9\xcd\xce\xc1\x182"'
Kn = [0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0]
# Despermuted[48]
PC2 = [14, 17, 11, 24, 1, 5, 3, 28, 15, 6, 21, 10, 23, 19, 12, 4, 26, 8, 16, 7, 27, 20, 13, 2, 41, 52, 31, 37, 47, 55, 30, 40, 51, 45, 33, 48, 44, 49, 39, 56, 34, 53, 46, 42, 50, 36, 29, 32]
# DesRotations
movnum = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]#对应16轮中每一轮的循环左移位数
def gen_key(C1,D1,k):
    tempc=C1
    tempd=D1
    for i in range(k):
        tempc = tempc[1:] + tempc[:1]
        tempd = tempd[1:] + tempd[:1]
    tempCD1=tempc+tempd
    tempkey=[]
    for i in range(len(PC2)):
        tempkey.append(tempCD1[PC2[i]-1])
    return (tempkey,tempCD1)#轮运算得到下一轮子密钥

def re_gen_key(C1,D1):
    tempc=C1[-1:]+C1[:-1]
    tempd=D1[-1:]+D1[:-1]
    tempCD1=tempc+tempd
    return tempCD1 #轮运算得到上一轮CD

d = pyDes.des("0"*8)
CD = ['*']*56

# 获得PC-2置换前的数据，即56位密钥，当然其中有8位我们依然是未知的
for i in range(len(PC2)):
    CD[PC2[i]-1] = Kn[i]

for i in range(256):
    # 遍历2^8种可能
    temp = CD[::]
    bi = bin(i)[2:].zfill(8)
    tot = 0
    for j in range(len(temp)):
        if temp[j] == '*':
            temp[j] = int(bi[tot])  # 将丢失的8位填充进去
            tot += 1

    # 回到初始密钥
    for j in range(sum(movnum[:8])):  # 逆向循环左移操作，回到最初的密钥形态
        temp = re_gen_key(temp[:28],temp[28:])

    tempK=[]
    Z = temp
    # 16轮迭代重新生成新的子密钥
    for j in range(16):
        tempx=gen_key(Z[:28],Z[28:],movnum[j])
        tempK.append(tempx[0])
        Z=tempx[1]
    d.Kn = tempK
    print(d.decrypt(enc))  # 使用子密钥解密消息